Les “Exchange-Traded Fund” (ETF) sont le meilleur moyen d’investir en bourse de façon diversifié et à faible frais. De plus, la liquidité est assurée par des “market maker” qui sont souvent des gros acteurs du marché (banques, fonds de gestion, …) ce qui renforce la confiance dans ce type de produit. Néanmoins, il rajoute des frais, un intermédiaire et donc un risque, aussi minime soit-il.
Dans cet article, nous allons essayer de neutraliser le risque des ETF. Un moyen simple consiste à se passer des ETF et investir sur les actions en direct. Cependant, si nous souhaitons reproduire le S&P 500, cela implique de devoir acheter les 500 entreprises en respectant la pondération. Cela peut s’avérer coûteux, mais à partir de quel capital est-ce possible ? De plus, est-ce vraiment nécessaire de reproduire le S&P 500 pour être diversifié, est-ce que le S&P 100 suffit ? Ou le S&P 20 ?
Dans une première partie, nous allons définir la notion d’indice boursier et d’ETF ainsi que leurs limites. Dans une seconde partie, nous formalisons le problème d’optimisation et nous présentons les données utilisées pour notre analyse. Dans un troisième partie, nous analysons les données à partir du cours boursier d’indices représentant un nombre restreint d’actions. Nous mesurons la volatilité de ces portefeuilles, constitués d’un échantillon d’actions appartement à l’indice. Enfin, nous concluons en donnant le nombre minimal d’actions à détenir en portefeuille, ainsi que le capital minimal nécessaire, pour s’approcher au plus près de la performance d’un indice.
Sommaire
1. Définitions
A. ETF
Un ETF (Exchange-Traded Fund), ou fonds négocié en bourse, est un type de fonds d’investissement qui regroupe un portefeuille d’actifs (actions, obligations, matières premières, etc.) et qui est coté en bourse, comme une action. Sa particularité est de répliquer la performance d’un indice boursier (par exemple, le S&P 500) ou d’un secteur spécifique.
Un ETF à l’avantage de pouvoir permettre une exposition, à faible frais (souvent quelques dixième de pourcent par an), une grande liquidité, et une diversification instantanée. Par exemple s’exposer à un indice mondial comme le MSCI World composé de plus de 3000 entreprises ! Autrement dit, un ETF permet de réduire le risque individuel liée à chaque action en ayant une plus grande liquidité qu’un fond classique. Pour plus de détails sur le fonctionnement de ce type de produits financiers j’ai réalisé un article détaillé sur le sujet.
B. Indice boursier
Un indice boursier est un indicateur qui mesure la performance d’un ensemble d’actions représentatives d’un marché, d’un secteur d’activité ou d’une région géographique. Il sert de référence pour évaluer l’évolution de ce marché ou secteur dans le temps. Chaque indice regroupe un certain nombre de titres (actions) sélectionnés selon des critères spécifiques, tels que la capitalisation boursière, la liquidité ou le secteur économique.
Un indice est composé d’un portefeuille théorique d’actions. Par exemple, le CAC 40 regroupe les 40 plus grandes entreprises cotées à la Bourse de Paris. Un indice est calculé en fonction de la valeur des actions qui le composent, selon des méthodes spécifiques (pondération par la capitalisation boursière, égalité de poids, etc.). Parmis les indice les plus connus nous retrouvons:
- CAC 40 (France) : Représente les 40 plus grandes capitalisations boursières françaises.
- Dow Jones (États-Unis) : Mesure la performance de 30 grandes entreprises américaines.
- S&P 500 (États-Unis) : Regroupe 500 grandes entreprises cotées aux États-Unis.
- Nikkei 225 (Japon) : Indice phare de la Bourse de Tokyo.
En résumé, un indice boursier est un outil essentiel pour les investisseurs et les analystes afin de suivre l’évolution des marchés financiers.
C. Les limites des ETF
Un ETF ne permet pas de réduire le risque du marché. Pour rappel, le risque est lié aux fluctuations du marché sur lequel nous investissons (marché actions, marché obligataires, …). Avec un ETF mais nous ne sommes diversifiés que sur une classe d’actif (sauf certains ETF très spécifiques). Seule une bonne allocation d’actif stratégique permet de minimiser ce risque, comme abordé dans cet article.
De plus, le turnover est souvent minimum au sein d’un indice. Si nous prenons l’indice MSCI World, le turnover est de 2%. Une fois le portefeuille établi avec les bons pourcentages entre les actions détenus en direct il n y a plus rien à faire ! A part sortir une ou plusieurs actions de l’indice et faire rentrer le ou les nouveaux entrants.
Fiscalement il peut parfois être plus intéressant de détenir les actions en direct en fonction des accords de double imposition établis avec la France et le pays ou le siège de l’action de l’entreprise est établie. Lorsque vous détenez un ETF, au yeux de l’impôt, c’est l’émetteur de l’ETF qui vous verse un dividendes. Les accords de double imposition s’effectuent en fonction de la domiciliation de l’ETF (souvent en Irlande).
Enfin, les ETF peuvent introduire un risque de contrepartie que ce soit pour la revente de celui-ci qui dépend de la liquidité offerte par les “market-maker” ou la détention des titres qui dépend de la société de gestion. De plus, vous n’êtes pas propriétaire des titres mais d’un fond qui détient de titres. Ce fonds peut parfois effectuer des prêts sur titre dans l’objectif de pouvoir réduire les frais de gestion ce qui augmente le risque en ajoutant une contrepartie pour le détenteur du fonds.
2. Le problème
A. Formalisation
Cette partie aura pour objectif de formaliser mathématiquement le problème, celle-ci peut être considérée comme complexe pour les moins familier au mathématiques. Néanmoins, j’invite tous les curieux à s’y pencher !
En supposant un portefeuille équipondéré composé de \( n \) actions avec \( n \in \mathbb{N} \). En supposant une volatilité annualisée du marché notée \( \sigma_{m} \) avec \( \sigma_{m} \in \mathbb{R} \) et \( \sigma_{m} \in [0; 1] \) et une volatilité individuelle pour chaque action notée \( \sigma_{i} \) avec \( \sigma_{i} \in \mathbb{R} \) et \( \sigma_{i} \in [0; 1] \) et \( i \in \mathbb{N} \). La volatilité du portefeuille, notée \( \sigma_{p} \), évolue suivant la formule (1).
\[
\sigma_p = \sqrt{\sigma_m^2 + \frac{1}{n} \sum_{i=0}^{n} \sigma_i^2} \qquad (1)
\]
Notre objectif est de trouver le seuil à partir duquel le nombre d’actions \( n \) permet d’obtenir un \( \sigma_{p} < \epsilon \) avec \( \epsilon \) un seuil fixé considéré comme suffisamment faible pour avoir la même performance que le marché.
En pratique les actions n’ont pas toutes la même volatilité. De plus, elles sont plus ou moins corrélées entre elles avec une corrélation qui évolue. Par exemple, deux actions totalement corrélées avec la même volatilité s’annulent et le portefeuille n’a plus de volatilité ! Enfin, les actions ne sont jamais équipondéré c’est le marché qui décide ce qui fait varier les capitalisations boursières. La formule (2) intègre ces nouveaux paramètres.
\[
\sigma_p = \sqrt{\sigma_m^2 + C \times \sum_{i=0}^{n} w_i \times \sigma_i} \qquad (2)
\]
\[ \text{avec}
\sum_{i=0}^{n} w_i = 1 \quad \text{et} \quad C \in [0,1] \quad \text{et} \quad C \in \mathbb{R}
\]
Nous notons \( w_{i} \) la pondération de chaque action \( i \in \mathbb{N} \) dans l’indice et \( C \) un facteur de corrélation globale. Identifier un facteur de corrélation entre chaque action deux à deux peut-être complexe. Par simplicité, nous utilisons un facteur \( C \) qui correspond à la corrélation moyenne entre toutes les actions. Si toutes les actions sont décorrélées entres elle alors \( C = 0 \) . Les actions du portefeuille neutralisent leur risque intrinsèque entres-elles et il ne reste que la volatilité du marché (le risque de marché). En revanche, si \( C = 1 \) les actions n’ont pas de corrélation entres-elles.
B. Les données
Pour effectuer notre analyse nous prenons comme référence, pour le marché actions, le S&P 500 “Total Return” qui est un l’indice phare américain comprenant les 500 plus grosses entreprises américaines. Nous utiliserons cet indice pour deux raisons :
- L’Indice couvre 50% de la capitalisation boursière mondiale. Les données des entreprises contenues dans l’indice sont donc facilement accessibles.
- L’indice comprend 500 entreprises ce qui est suffisant pour évaluer l’écart qui peut exister entre une reproduction totale (500 entreprises) et une reproduction partielle (10 ou 20 par exemple).
Les données utilisées seront issues de trois sources:
- Robert Shiller : professeur à l’université de Yale et prix Nobel d’économie, il met à disposition des données historiques pour la recherche académique (inflation, bon du Trésor U.S. et données historiques du S&P 500).
- Standard and Poor’s : la société nous fournit un ensemble d’indices permettant d’affiner notre analyse sur un historique de 10 ans (au-delà il faut payer).
- Yahoo Finance : nous pourrons y récupérer les cours boursiers de chaque entreprise. Nous pouvons également récupérer les données récentes du S&P 500.
3. Analyse de données
A. Objectif
Nous allons essayer de déterminer le nombre d’actions à détenir afin de s’approcher au plus près de la performance du marché en termes de rendement et de volatilité. D’après la théorie moderne de la construction de portefeuille de Harry Markowitz, la corrélation des actifs influent sur la volatilité du portefeuille.
Un première stratégie pourrait être de sélectionner des actions dé-corrélées afin de minimiser la volatilité et de maximiser le rendement (trouver l’“efficient frontier”). Il faut supposer que les actions sélectionnées continueront de conserver la même corrélation. Des corrélations trop changeantes impacteraient la volatilité du portefeuille et obligeraient à des entrées-sorties sur la marché trop fréquentes (et donc des frais !). En pratique, ces corrélations peuvent évoluer en fonction de la stratégie des entreprises et de l’attrait des investisseurs pour ces sociétés (par des biais émotionnels ou une rationalité). Effectuer une analyse en prenant un sous échantillons d’actions corrélées n’est donc pas viable sur le long terme.
Pour éviter ces biais, une seconde stratégie pourrait être de sélectionner les actions de façon aléatoire parmi les 500 actions. Nous prenons une période d’un mois et nous regardons la volatilité du portefeuille constitué avec des actions prises aléatoirement en respectant la pondération du portefeuille initial. Par exemple, si nous sélectionnons 2 actions simulées qui ressemblent à Apple et Microsoft avec un pondération respective de 6% et 2% dans le S&P 500 la pondération dans le portefeuille à deux actions sera de respectivement 75% et 25%. Nous répétons l’opération 1000 fois (simulation de Monte Carlo) afin d’obtenir une estimation de la volatilité de chaque portefeuilles avec 1, 2, 3, … actions.
La seconde stratégie serait la plus viable statistiquement mais nécessite l’accès à des bases et un historique de données qui ont un coût. Il faut prendre en compte les entrées et sorties des valeurs de l’indice au cours du temps et récupérer le cours boursier d’actions d’entreprise disparues, fusionnées avec d’autres ou scindées en plusieurs entreprises. Pour pallier cette limite, nous allons utiliser trois stratégies et les combiner afin d’avoir une réponse suffisamment proche de la réalité :
- Simulation avec des hypothèses : en reprenant la formule (2), l’objectif va être d’appliquer des hypothèses de corrélation et de distribution de la répartition des action au sein de l’indice. Nous pouvons visualiser l’impact sur les résultats en fonction des différentes hypothèses.
- Simulation à partir des indices : il existe des indices comprenant un sous ensemble plus restreint d’actions de l’indice que nous considérons comme représentatif du marché actions (le S&P 500). Ces sous-indices (S&P Top Select 20, S&P 100, S&P Top Select 50) peuvent servir à mesurer la volatilité et le rendement pour un nombre d’actions restreint.
- Mesure à partir des actions individuelles : la composition des indices est connue. Il est possible de récupérer des informations statistiques sur chacune des actions de l’indice pour en déduire une mesure plus précise de la volatilité en fonction du nombre d’actions choisies.
B. Volatilité
i. Le marché ( \( \sigma_{m} \) )
Pour pouvoir simuler le cours des actions du S&P 500 nous allons nous baser sur la distribution de la rentabilité mensuelle historique du S&P 500 “Total Return” (dividendes réinvestis) au nominal. Comme abordé dans cet article, la distribution du S&P 500 peut être approximée avec une distribution de t-Student à 2 degrés de liberté. Pour simplifier le calcul de la variance (et donc de la volatilité), nous utilisons une distribution suivant une loi normale. La Figure 1 montre la distribution de la rentabilité mensuelle du S&P 500 “Total Return” (dividendes réinvestis) approximée par une loi normale entre 1872 et 2024.
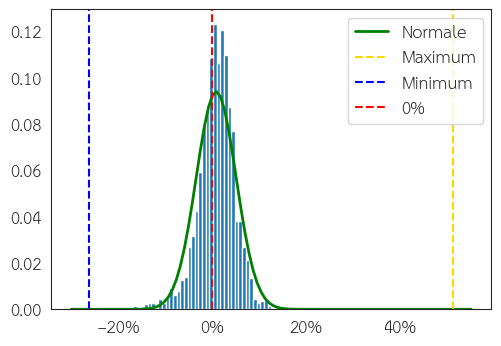
Figure 1 : Distribution de t-Student (en orange) représentée à partir de la rentabilité mensuelle au nominal du S&P 500 entre 1872 et 2024. Sources : Robert Shiller, Yahoo Finance.
La Figure 2 montre l’évolution de la volatilité annuelle et de la rentabilité mensuelle entre 1872 et 2024. Nous pouvons voir que le comportement des marchés ainsi que les acteurs ont fortement évolué. C’est la théorie des marchés adaptatif du Pr. Andrew Lo professeur au Massachusett Institut Technology (MIT).
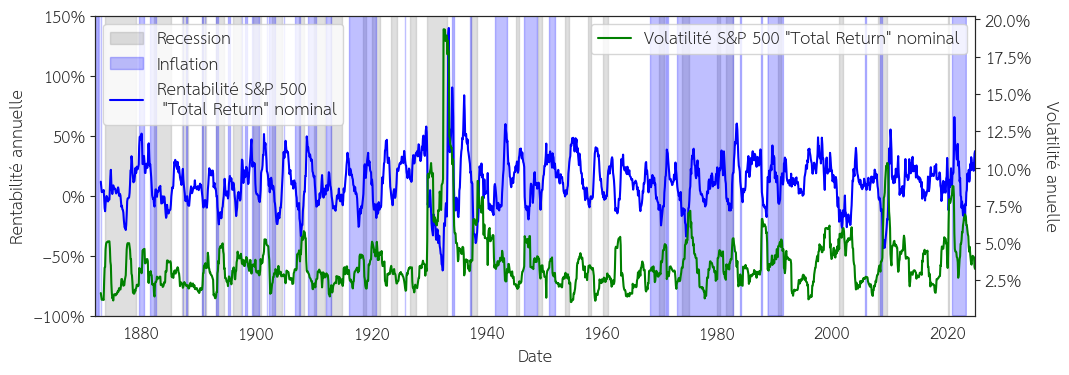
Figure 2 : Évolution de la rentabilité mensuelle et de la volatilité annuelle au nominal du S&P 500 entre 1872 et 2024. Sources : FRED, Robert Shiller, Yahoo Finance.
Par exemple, si nous regardons la volatilité est la rentabilité annuelle du S&P 500 nous pouvons constater que la chute de 1929 ne sait pas reproduite. Elle a statistiquement moins de chance de se reproduire car les facteurs déclencheurs de cette crise sont aujourd’hui contrôlés par des mécanismes de régulation. Nous pouvons également noter une baisse importante de la volatilité annuelle après les années 1990. Il faut donc garder en tête que la mesure de la volatilité utilisée pour notre analyse (et également de nombreux articles de recherche) est biaisée.
Pour faciliter notre analyse, Standard and Poor’s fournit d’autres indices comme le :
- S&P Top Select 20 : il est composé des 20 plus grandes sociétés cotées sur les bourses américaines de l’indice S&P 500.
- S&P Top Select 50 : il est composé des 50 plus grandes sociétés cotées sur les bourses américaines de l’indice S&P 500.
- S&P 100 : il est composé des 100 plus grandes sociétés cotées sur les bourses américaines de l’indice S&P 500.
A partir de ces indices, il est facilement possible de calculer la volatilité et donc déterminer facilement l’écart qui peut exister entre le marché et un nombre restreint d’actions sélectionnées. Attention, l’historique accessible est de seulement 10 ans ce qui peut biaiser notre analyse en fonction de l’historique utilisé pour calculer la volatilité du marché.
ii. Les actions \( \sigma_{i} \)
Le dernier paramètres à estimer est la volatilité de chaque action. Un moyen simple serait de récupérer les données de chaque action qui compose l’indice ainsi que leur historique de données afin de mesurer la volatilité de chacune d’entre elles.
Cependant, il faut garder en tête que cette volatilité évolue. Une action, lorsqu’elle est introduite en bourse, peut être une petite capitalisation avec une volatilité supérieure à ce qu’elle serait en étant une grosse capitalisation. De plus, la volatilité peut évoluer au cours du temps en fonction de la macro-économie ou de la micro-économie liée à l’entreprise. La Figure 3 montre la distribution de la volatilité et de la rentabilité mesurée sur les données historiques des 20, 50, 100 et 500 premières entreprises que composent le S&P 500.
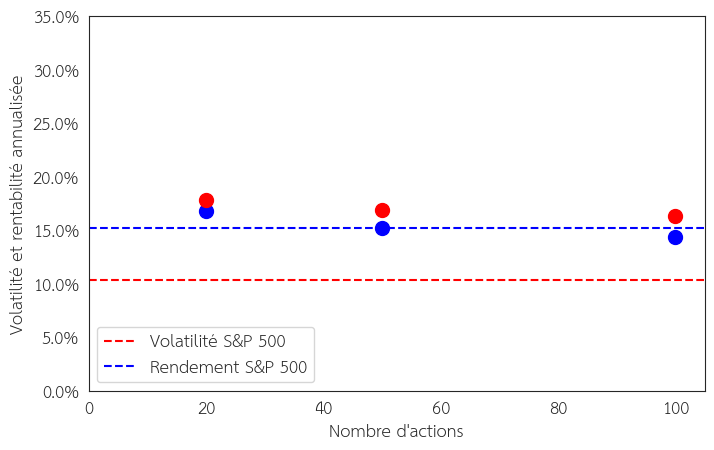
Figure 3 : Distribution de la volatilité et de la rentabilité mesurée sur les données historiques des 20, 50, 100 et 500 entreprises que composent le S&P 500 (entre mars 2015 et mars 2025). Sources : Slick Chart, Yahoo Finance.
C. Corrélation des actions (\(C\) )
Nous pouvons supposer que la popularisation des ETF accentue l’effet de corrélation entre les actions ce qui fait augmenter la valeur de \( C \). Cette valeur étant difficile à estimer car celle-ci peut également dépendre de facteurs macro-économique. Des secteurs non corrélés peuvent le devenir subitement suivant le contexte macro-économique. Nous prenons un espace de valeur allant de 0 à 1 avec 0 représentant une dé-corrélation totale entre les actions ce qui annule leur volatilité entre elles et 1 une corrélation accentuée .
D. Pondération des actions ( \( w_{i}\) )
Pour déterminer la pondération de chaque action dans l’indice nous pouvons nous baser sur le ”Matthew Effect” ou l’effet Mathieu en français. Cet effet peut se traduire par la phrase “Winners takes all” du livre eponymes. Nommé par le sociologue américain Robert K. Merton en 1968, il désigne un phénomène de concentration des avantages, où « les riches deviennent plus riches et les pauvres deviennent plus pauvres ». Ce concept s’applique à divers domaines, notamment la science, l’économie et l’éducation.
Autrement dit, la distribution des poids des actions d’un indice suit une loi exponentielle avec une forte concentration sur les valeurs de l’indice et une décroissance rapide. La Figure 4 permet de visualiser la distribution des pondérations des actions en suivant une loi exponentielle simulée comparé à la distribution actuelle des actions des poids de l’indice.
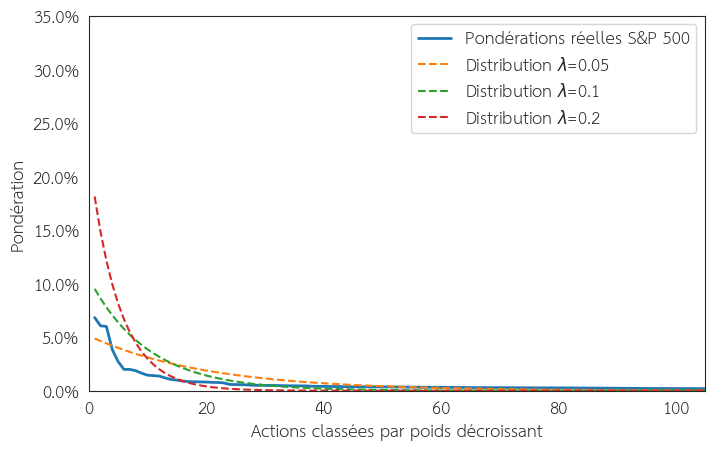
Figure 4 : Répartition des poids des actions en suivant des lois exponentielles simulés avec différents paramètres comparés à la vraie distribution des actions du S&P 500 (mars 2025). Source: Slick Chart.
E. Résultats
La Figure 5 montre la volatilité du portefeuille en fonction du nombre d’actions sélectionnées parmi les premières valeurs contenues dans l’indice. Différentes hypothèses de concentration d’indice sont appliquées. La volatilité utilisée pour chaque action est celle officiellement mesurée sur les données historiques de chaque action au cours des trois derniers mois (mars, février et janvier 2025). Les pondérations évoluent au cours du temps, or nous utilisons des pondérations fixes pour estimer la volatilité du portefeuille. Pour cela, nous prenons une période d’évaluation courte et nous extrapolons afin de minimiser l’écart qui peut exister avec la véritable volatilité mesuré.
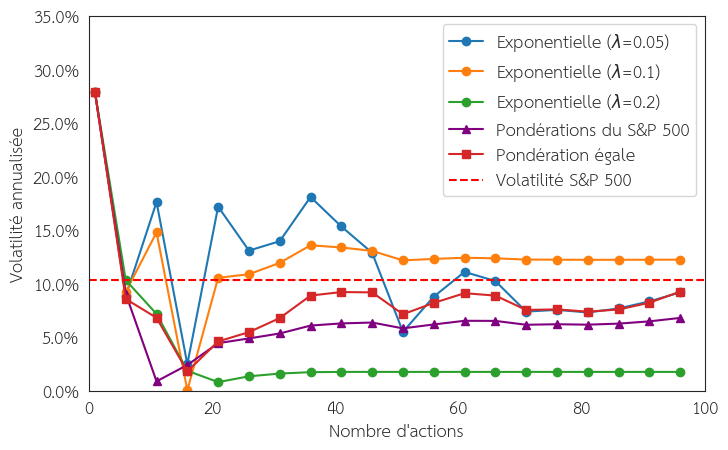
Figure 5 : Volatilité du portefeuille en fonction du nombre d’actions sélectionnées dans l’indice en fonction de différentes hypothèses de concentration d’indice (mars 2025). Sources : Slick Chart, Yahoo Finance.
Nous pouvons voir que plus nous augmentons le nombre d’actions dans le portefeuille et plus la volatilité du portefeuille diminue en s’approchant de la volatilité du marché. Cependant, il n’est pas nécessaire d’avoir les 500 actions pour avoir une volatilité proche de l’indice, une trentaine d’actions suffit et nous permet d’avoir un écart de volatilité de 2-3 %. Nous pouvons également voir que la concentration des indices à un impact important sur la performance du portefeuille. Lorsque la distribution des poids des actions dans l’indice est plus étalé ( \( \lambda = 0.05 \)) la volatilité est plus hiératique et il est nécessaire d’avoir un nombre d’actions plus important afin d’approcher une stabilité et donc la volatilité du S&P 500.
La corrélation entre les actions à un impact important sur le nombre d’actions. La prolifération des ETF tend à augmenter la corrélation entre les actions au sein de l’indice comme évoqué dans article. Plus la corrélation augmente entre les actions de l’indice et moins il est nécessaire d’avoir un nombre d’actions important pour s’approcher de la performance de l’indice et éviter de dévier de celui-ci (voir formule (2)).
F. Conclusion
D’après notre analyse, détenir les 20-30 premières actions de notre indice est suffisant pour obtenir une diversification proche du marché actions représenté par le S&P 500. Les pistes de réflexion qui peuvent permettre de réduire la volatilité du portefeuille plus rapidement peuvent être :
- De sélectionner des actions les plus corrélés au marché (à l’indice S&P 500), avec un qui soit le plus proche de 1. Le plus souvent, les actions qui ont la plus forte capitalisation ont une corrélation proche du marché en particulier si l’indice est concentré sur les premières actions.
- De sélectionner des actions avec une faible volatilité. Cette faible volatilité traduit souvent une grosse capitalisation avec des revenus stables et facilement prévisible avec un faible endettement. Autrement dit, cela revient à sélectionner des actions répondant au critère “Quality” (faible endettement, fort ROE, hausse croissante et continu des revenus).
Théoriquement, plus nous respectons ces critères et moins le nombre d’actions à détenir pour approcher la performance du marché est nécessaire. Notons que la quantité d’actions déterminer s’est basée sur des hypothèses qui peuvent être amenées à évoluer en fonction de l’évolution du marché et de ces acteurs. Pour pouvoir sélectionner ces actions j’ai une page dédiée, mise à jour quotidiennement, qui référence les actions répondant au critère Quality calculé par MSCI.
4. Limite de notre approche
Le nombre d’actions sélectionné est principalement focalisé sur les premières valeurs de l’indice. Prendre les valeurs aléatoirement n’aurait peut-être pas permis d’avoir les mêmes performances. Il faut mettre ça en perspective vis-à-vis de la concentration des indices actuels. Les 20 premières lignes de l’indice couvre 40% de l’ indice et les 20 derniers seulement 0,2%. Historiquement cela n’a pas tout le temps était le cas comme c’est visible sur la Figure 6.
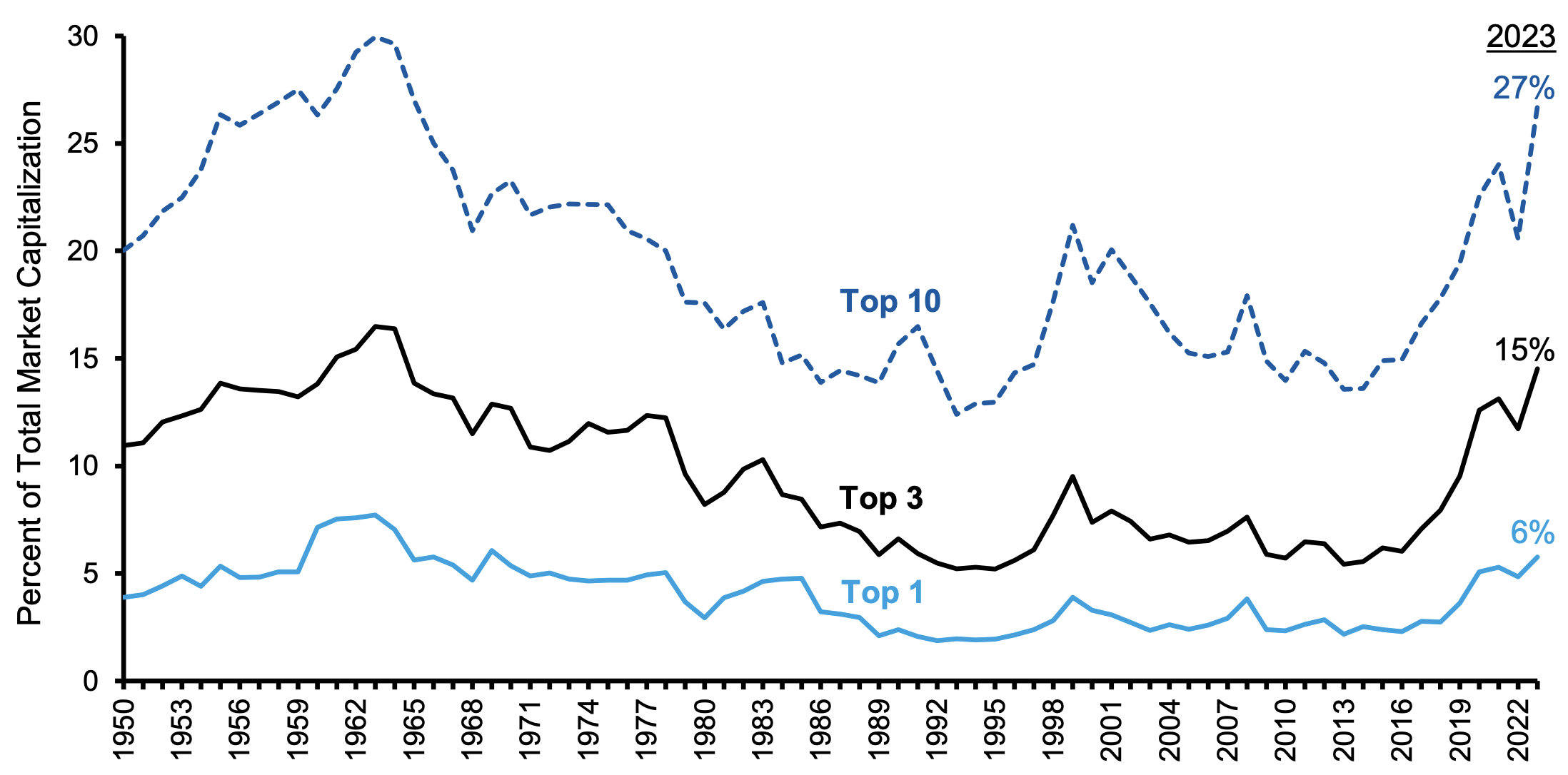
Figure 6 : Concentration des composants du MSCI World entre mars 2002 et janvier 2023. Source : Morgan Stanley.
Le dégonflement de la bulle des années 2000 à réduit la concentration de l’indice. Si les premières lignes couvrent 40% de l’indice, nous pouvons expliquer 40% de la volatilité de l’indice avec ces lignes. Ce qui est important ce n’est pas le nombre, mais le pourcentage de l’indice couvert par les actions sélectionnées. Plus les actions sélectionnées couvrent une partie de l’indice et plus nous nous approchons des performances de l’indice. Si la concentration baisse il faudra peut être prendre plus d’actions pour pouvoir compenser cette effet de répartitions.
5. Mise en pratique
Nous savons, grâce à l’analyse effectuée dans la sous section précédente, que 30 actions suffisent pour obtenir des performances proches d’un indice (comme le S&P 500), avec une erreur de 2-3%. Cet écart de performance doit être jugé au regard de la détention d’ETF (frais, accords de non double imposition sur les dividendes, enveloppe fiscale, …). Sachant que la performance est majoritairement concentrée sur les premières valeurs, cela revient à sélectionner, par échantillonnage, les premières valeurs de l’indice, en fonction du capital disponible.
Un moyen empirique de trouver la solution est de trouver l’action qui à le prix maximum parmi les 30 premiers composants de l’indice S&P 500. Nous supposons qu’il n’est pas possible d’acheter des fractions d’actions. Il faut donc donc pouvoir acheter l’action la plus chère sans déséquilibrer totalement le portefeuille. En utilisant les listes des composants fournis par Slick Chart nous pouvons voir que l’action la plus chère est Netflix à 967,88 $ dollars (prix mesuré en mars 2025). Nous savons que Netflix pèsent 1,73% sur les 30 premières valeurs de l’indice (mesure effectuée à partir du .csv fourni par l’émetteur). La première action, Apple, pèse 6,83% dans l’indice et coûte 219,13 $.
Par un simple produit en croix, nous savons qu’il faut être capable de mettre 3821 $ sur Apple pour garder la même pondération que dans l’indice ( \( \frac{6.83 \times 967.88}{1,73} =3821 $\)). En répétant le calcul pour chaque action, nous pouvons déterminer la somme minimale nécessaire à posséder pour s’approcher de l’indice. La Figure 7 montre le capital minimal nécessaire à détenir en fonction du nombre d’actions en portefeuille afin de ne pas trop déséquilibrer l’allocation.
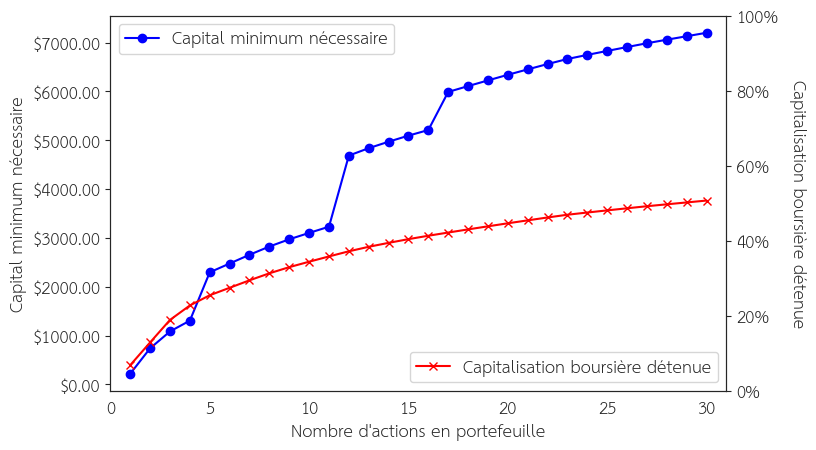
Figure 7 : Capital minimum nécessaire à détenir en fonction du nombre d’actions en portefeuille (mars 2025). Source : Slick Chart.
Une fois le portefeuille constitué, il existe un écart de pondération car les actions ne peuvent pas être fractionnées. La Figure 8 montre l’écart moyen de pondération de pondération entre l’indice et le portefeuille en investissant le capital minimal.
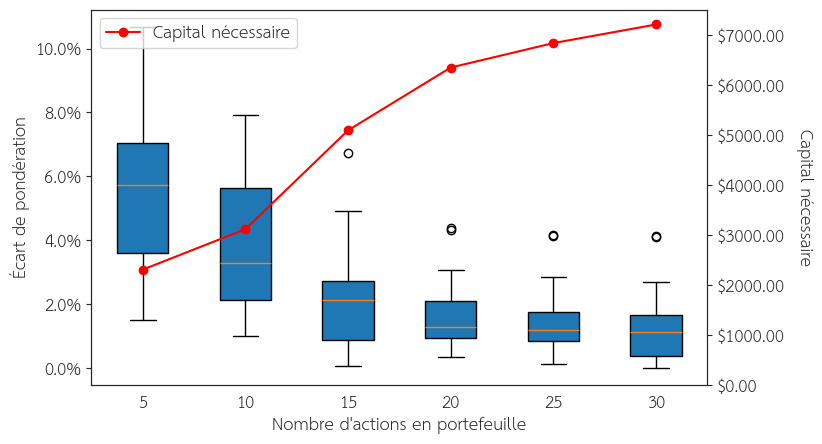
Figure 8 : Distribution de l’écart de pondération entre le portefeuille et l’indice en fonction du nombre d’actions (mars 2025). Source : Slick Chart.
Pour pouvoir approcher la performance de l’indice S&P 500 il faut posséder un capital d’environ 10 000 € en supposant que l’écart de performance entre l’indice et le portefeuille est suffisant. Autrement dit, aujourd’hui, à partir de 10 000 euros investir en ETF peut s’avérer moins rentable qu’investir directement sur des actions en direct. Cette affirmation peut évoluer en fonction de l’évolution des marchés pouvant impacter la concentration des indices et leur corrélation.
6. Conclusion
Dans cet article, nous avons vu que les ETF actions pouvaient présenter plus de risque (même si négligeable) que la détention d’actions en direct (risque de contreparties, prêt sur titre, …). Pour réduire ce risque, nous avons cherché à déterminer le nombre d’actions minimum à détenir en portefeuille afin d’approcher la performance de l’indice S&P 500. Nous avons simuler un indice similaire au S&P 500 à partir des données historiques. Ensuite, nous avons déterminé le capital minimal nécessaire en fonction du nombre d’actions que nous souhaitons détenir et de l’erreur moyenne de pondération que nous commettons par rapport à l’indice. Nous estimons que détenir 30 actions avec un capital minimum de 10 000 € environ est suffisant pour se passer d’ETF.
